Meilisearch Indexes Embeddings 7x Faster with Binary Quantization
Note
This is one blog post in a series:
- Spotify-Inspired: Elevating Meilisearch with Hybrid Search and Rust,
- Multithreading and Memory-Mapping: Refining ANN Performance with Arroy,
- Meilisearch Expands Search Power with Arroy's Filtered Disk ANN,
- How Meilisearch Updates a Millions Vector Embeddings Database in Under a Minute.
- Meilisearch Indexes Embeddings 7x Faster with Binary Quantization.
For the past year at Meilisearch, we’ve been working hard on hybrid search, which mixes keyword search with semantic search using Arroy: our vector store, based on a Spotify technology. A vector store is a data structure that efficiently stores embeddings (vectors) for fast and relevant retrieval, called Approximate Nearest Neighbors (ANN) search.
When our customers started to use arroy heavily, some of them started reaching the machine limits. For example, for a customer with a 768 dimensions model, we found out that we couldn’t index more than 15M of embeddings on a machine with 64GiB of RAM.
Binary Quantization to the Rescue
The concept behind this elaborate term is that we are going to quantize the embeddings. Quantizing a number involves spreading it into a defined number of values; for binary quantization, two values can be represented on a single bit, e.g., 0.2561 becomes 1, and -0.568 becomes -1.
This implies that we could convert a 32-bit float number into a 1-bit number, which would divide the disk and RAM usage by 32. That would mean we could index up to 480M embeddings with 64GiB of RAM, instead of being limited to 15M embeddings.
An issue we faced is that bits cannot represent -1 and 1 but only 0 and 1. We had to use some tricks to make it work and fake 0s into -1s in our computations. For example, one of the functions that we had to optimize a lot was the function in charge of converting a binary quantized vector to 32-bit float vectors.
We do not publicly expose raw quantized embeddings and utilize this function to provide real 32-bit float embeddings to the users. However, the primary reason for converting 1-bit quantized embeddings to 32-bit floats is to ensure high precision when generating hyperplanes to group embeddings together and maintaining relevant ANNs.
Converting a quantized embedding back to 32-bit floating points takes up to 24.21s on a 1m53s run.
Below is the SIMD neon-specific version of this function. It processes raw bytes corresponding to a 1-bit quantized embedding, converting them into a properly aligned 32-bit float embedding. Using masks, the function separates the low and high bits, processing them in batches of four in 128-bit registers, which are then transformed into four 32-bit floats. These values are collectively written to the output vector.
unsafe fn to_vec_neon(bytes: &[u8]) -> Vec<f32> {
let mut output: Vec<f32> = vec![0.0; bytes.len() / u32::BITS];
let output_ptr = output.as_mut_ptr();
let low_mask = [0b_0000_0001, 0b_0000_0010, 0b_0000_0100, 0b_0000_1000];
let high_mask = [0b_0001_0000, 0b_0010_0000, 0b_0100_0000, 0b_1000_0000];
let ones = unsafe { vld1q_dup_f32(&1.0) };
let minus = unsafe { vld1q_dup_f32(&-1.0) };
for (current_byte, base) in bytes.iter().enumerate() {
unsafe {
let base = *base as u32;
let base = vld1q_dup_u32(&base);
for (i, mask) in [low_mask, high_mask].iter().enumerate() {
let mask = vld1q_u32(mask.as_ptr());
let mask = vandq_u32(base, mask);
// 0xffffffff if equal to zero and 0x00000000 otherwise
let mask = vceqzq_u32(mask);
let lane = vbslq_f32(mask, minus, ones);
let offset = output_ptr.add(current_byte * 8 + i * 4);
vst1q_f32(offset, lane);
}
}
}
output
}Daniel Lemire doesn't seem to have found a better algorithm 🤭
The Results
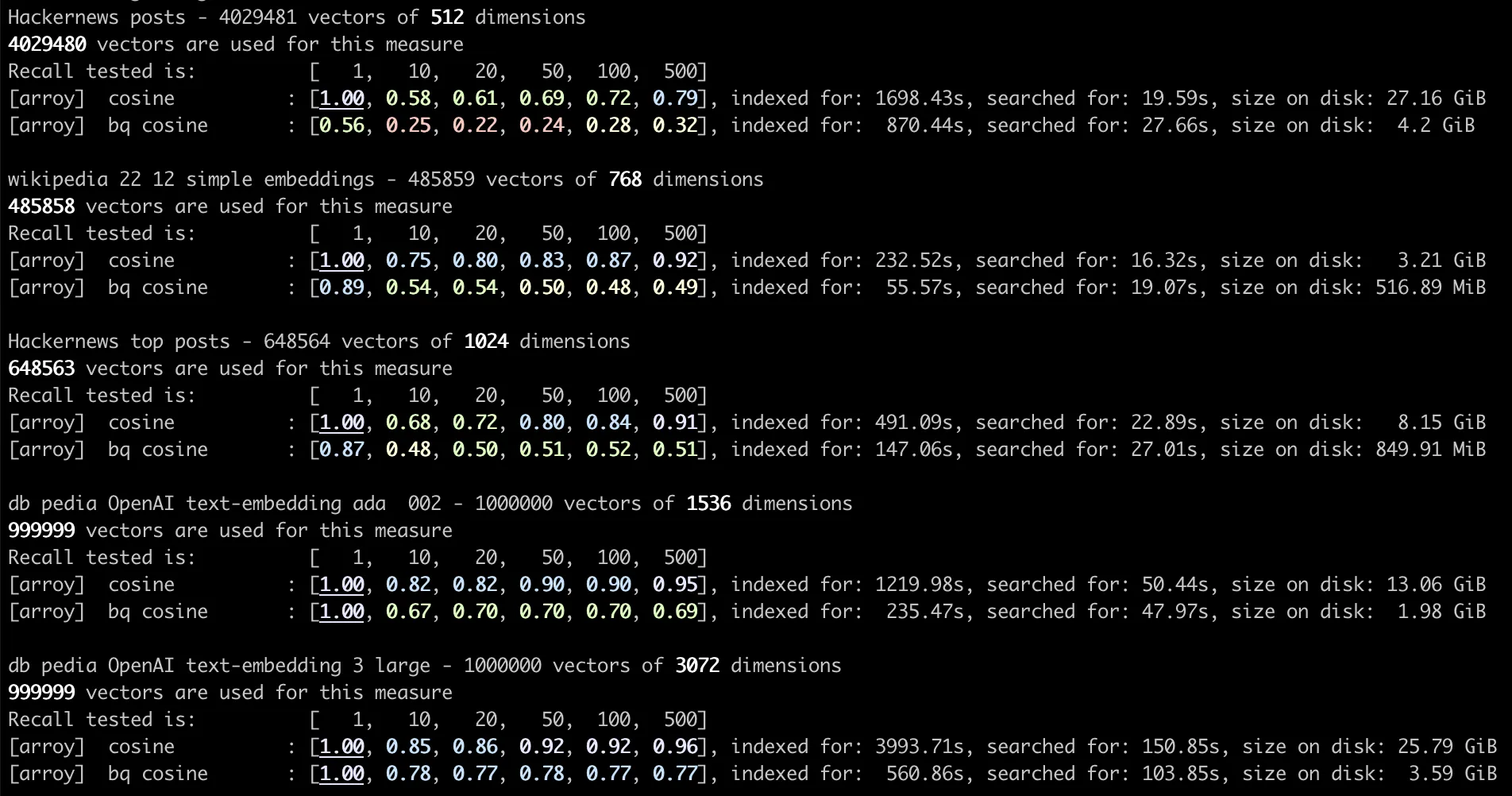
We chatted about the theoretical benefits of this approach earlier, but how does it work out in real life? Here are different tables summarizing the results for you.
Embeddings with 1024 Dimensions
When examining small embeddings, we can observe a significant impact on relevancy due to binary quantization. The primary advantages of this approach lie in faster insertion times and reduced storage requirements. It is not advisable to enable this feature for small embeddings, as they already occupy minimal disk space. Storing over four million 1024-dimensional embeddings requires just 8 GiB of disk space.
| Version | Recall @1 | Recall @20 | Recall @100 | Indexing time | Search time | On disk size |
|---|---|---|---|---|---|---|
| Cosine | 1.00 | 0.72 | 0.84 | 491s | 23s | 8 GiB |
| Binary Quantized Cosine | 0.87 | 0.50 | 0.52 | 147s | 27s | 850 MiB |
Embeddings with 1536 Dimensions
Binary quantization proves advantageous for managing larger embeddings. It significantly reduces search times, utilizing just 15% of the original disk space. Indexing about 500,000 1536-dimensional embeddings is achieved in a quarter of the time. Despite this, there remains a noticeable impact on relevancy...
| Version | Recall @1 | Recall @20 | Recall @100 | Indexing time | Search time | On disk size |
|---|---|---|---|---|---|---|
| Cosine | 1.00 | 0.82 | 0.90 | 1219s | 50s | 13 GiB |
| Binary Quantized Cosine | 1.00 | 0.70 | 0.70 | 235s | 47s | 2 GiB |
Embeddings with 3072 Dimensions
The impact of binary quantization on large embeddings is evident. While relevance may be slightly affected, the reduction in disk usage, search time, and indexing time is significant. Being able to store the same number of embeddings with just 15% of the space and index 6 times faster is a major achievement! It takes half as much disk space to store a million 3072-dimensional binary quantized embeddings than four million 1024-dimensional embeddings.
| Version | Recall @1 | Recall @20 | Recall @100 | Indexing time | Search time | On disk size |
|---|---|---|---|---|---|---|
| Cosine | 1.00 | 0.86 | 0.92 | 4000s | 150s | 26 GiB |
| Binary Quantized Cosine | 1.00 | 0.77 | 0.77 | 560s | 100s | 4 GiB |
Conclusion
The impact of binary quantization on recall was expected to decrease, given the reduced information in the algorithm. However, for datasets with over 1500 dimensions, the impact on recall is relatively minor compared to the significant benefits in disk space and indexing speed.
In practice, we observed that space utilization decreased not by 32 times but by just 15% of the original space, a notable achievement. This is primarily due to arroy storing not only user vectors but also internal nodes for efficient searching. Split nodes (hyperplanes) are retained as full 32-bit floats to maintain precision.
- Indexing speed improves nearly 5 times with 1536 dimensions and about 7 times with 3072 dimensions.
- Disk size shrinks to around 6.5 times smaller.
- Search time shows slight improvements for embeddings starting at 1536 dimensions.
We recommend using Meilisearch/arroy's binary quantization feature for OpenAI users with large embeddings. In an upcoming article, we will compare Meilisearch/arroy with competitors, focusing on our Filtered DiskANN feature. Stay tuned!